집합론
- 조선대학교
- 김진홍
페이스북
트위터
카카오톡
네이버밴드
링크복사
-
- 주제분류
- 자연과학 >수학ㆍ물리ㆍ천문ㆍ지리 >수학
-
- 강의학기
- 2021년 2학기
-
- 조회수
- 18,172
-
- 강의계획서
- 강의계획서
본 과목의 목표는 해석학, 기하학, 위상수학을 공부하기 위한 기초와 수학적인 논리성을 확립하는 것에 있다. 수리논리학 과목에서 학습했던 집합의 개념, 관계와 함수 등을 바탕으로 가부번집합과 비가부번집합, 기수와 그것의 셈, 선택공리, 조른의 보조정리, 하우스도르프 극대원리, 순서수와 덧셈 및 곱셈 등을 학습한다.
차시별 강의
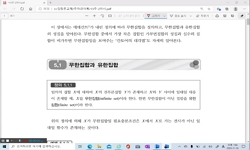
| 1. | |
무한집합과 유한집합 | 무한집합과 유한집합의 정의, 무한집합과 유한집합의 예, 집합의 대등 |  |
|
무한집합과 유한집합 | 무한집합과 유한집합의 정의, 무한집합과 유한집합의 예, 집합의 대등 | |
|
|
무한집합과 유한집합 | 무한집합과 유한집합의 정의, 무한집합과 유한집합의 예, 집합의 대등 | |
|
| 2. | |
가부번집합과 비가부번집합 | 가부번집합과 비가부번 무한집합의 정의, 무한집합의 판별법과 그 응용 | |
|
가부번집합과 비가부번집합 | 가부번집합과 비가부번 무한집합의 정의, 무한집합의 판별법과 그 응용 | |
|
|
가부번집합과 비가부번집합 | 가부번집합과 비가부번 무한집합의 정의, 무한집합의 판별법과 그 응용 | |
|
| 3. | |
기수와 기수의 대소 | 기수의 정의, 기수의 대소와 그 응용 | |
|
기수와 기수의 대소 | 기수의 정의, 기수의 대소와 그 응용 | |
|
|
기수와 기수의 대소 | 기수의 정의, 기수의 대소와 그 응용 | |
|
| 4. | |
칸토어-슈뢰더-베른슈타인 정리 | 칸토어-슈뢰더-베른슈타인 정리, 칸토어 정리, 칸토어 정의의 응용 | |
|
칸토어-슈뢰더-베른슈타인 정리 | 칸토어-슈뢰더-베른슈타인 정리, 칸토어 정리, 칸토어 정의의 응용 | |
|
| 5. | |
기수의 연산 – 덧셈과 곱셈 | 기수의 덧셈의 정의, 기수의 곱셈의 정의, 기수의 연산과 그 응용 | |
|
기수의 연산 – 덧셈과 곱셈 | 기수의 덧셈의 정의, 기수의 곱셈의 정의, 기수의 연산과 그 응용 | |
|
|
기수의 연산 – 덧셈과 곱셈 | 기수의 덧셈의 정의, 기수의 곱셈의 정의, 기수의 연산과 그 응용 | |
|
| 6. | |
기수의 연산 - 거듭제곱 | 기수의 거듭제곱의 정의, 거듭제곱 개념의 예와 구체적인 응용 | |
|
기수의 연산 - 거듭제곱 | 기수의 거듭제곱의 정의, 거듭제곱 개념의 예와 구체적인 응용 | |
|
|
기수의 연산 - 거듭제곱 | 기수의 거듭제곱의 정의, 거듭제곱 개념의 예와 구체적인 응용 | |
|
| 7. | |
기수연산의 응용 | 기수 연산의 구체적인 응용 | |
|
기수연산의 응용 | 기수 연산의 구체적인 응용 | |
|
|
기수연산의 응용 | 기수 연산의 구체적인 응용 | |
|
| 8. | |
부분순서집합과 조른의 보조정리 | 부분순서집합, 전순서집합, 조른의 보조정리와 그 응용, 조른의 보조정리와 하우스도르프 극대원리와의 관계 | |
|
부분순서집합과 조른의 보조정리 | 부분순서집합, 전순서집합, 조른의 보조정리와 그 응용, 조른의 보조정리와 하우스도르프 극대원리와의 관계 | |
|
|
부분순서집합과 조른의 보조정리 | 부분순서집합, 전순서집합, 조른의 보조정리와 그 응용, 조른의 보조정리와 하우스도르프 극대원리와의 관계 | |
|
| 9. | |
정렬원리 | 정렬원리의 정의와 응용, 선택공리, 조른의 보조정리, 하우스도르프 극대원리 등의 동치성 | |
|
정렬원리 | 정렬원리의 정의와 응용, 선택공리, 조른의 보조정리, 하우스도르프 극대원리 등의 동치성 | |
|
|
정렬원리 | 정렬원리의 정의와 응용, 선택공리, 조른의 보조정리, 하우스도르프 극대원리 등의 동치성 | |
|
| 10. | |
초한귀납법의 원리 | 초한귀납법의 원리, 초한귀납법의 원리와 그 응용 | |
|
초한귀납법의 원리 | 초한귀납법의 원리, 초한귀납법의 원리와 그 응용 | |
|
|
초한귀납법의 원리 | 초한귀납법의 원리, 초한귀납법의 원리와 그 응용 | |
|
| 11. | |
순서보존사상 | 순서보존사상과 절편과의 관계 | |
|
순서보존사상 | 순서보존사상과 절편과의 관계 | |
|
|
순서보존사상 | 순서보존사상과 절편과의 관계 | |
|
| 12. | |
순서수와 그 대소 | 순서수의 정의, 순서수의 대소와 그 응용 | |
|
순서수와 그 대소 | 순서수의 정의, 순서수의 대소와 그 응용 | |
|
|
순서수와 그 대소 | 순서수의 정의, 순서수의 대소와 그 응용 | |
|
| 13. | |
순서수의 연산 - 덧셈 | 덧셈의 정의, 순서수의 덧셈과 그 응용 | |
|
순서수의 연산 - 덧셈 | 덧셈의 정의, 순서수의 덧셈과 그 응용 | |
|
|
순서수의 연산 - 덧셈 | 덧셈의 정의, 순서수의 덧셈과 그 응용 | |
|
| 14. | |
순서수의 연산 - 곱셈 | 곱셈의 정의, 순서수의 덧셈과 그 응용, 브랠리-포르티 역설 | |
|
순서수의 연산 - 곱셈 | 곱셈의 정의, 순서수의 덧셈과 그 응용, 브랠리-포르티 역설 | |
연관 자료
